これは,
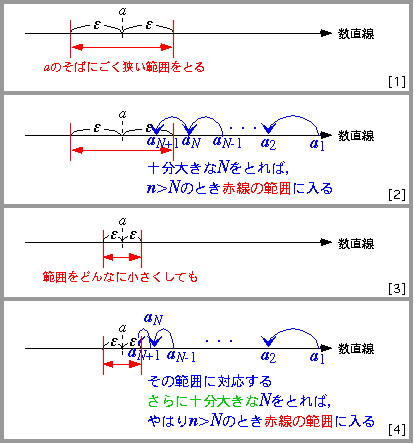
aのまわりにどんなに狭い区間[a-ε,
a+ε]をとっても,
十分大きな番号Nをとれば,
N番より大きい番号nのanでは,anとaの隔たりはεより小さくできる
という意味です.
これを「数学語」では
![]()
と書き,この考え方をε-N論法といいます.
下の「4コマ漫画」で,その意味をよく考えてみてください.
同様に,「n→∞の時,数列anが∞に発散する」とは
どんなに大きな数Gを持ってきても,
十分大きな番号Nをとれば,
N番より大きい番号nのanでは,anはGより大きくできる
という意味です.




1.問2および提出問題では,この数列が単調減少していることは明らかとして使っています.
同様に問3ではこの数列が単調増加していることは明らかとして使っています.
2.各証明ではいちいち「絶対値がεより小さい」「絶対値がGより大きい」という表現を使っています.
問2,3,提出問題ではan>0は明らかですが,そうでない場合も考慮に入れているからです.