
ある生産工程において,正常な工程が翌日以上をおこす確率は0.2,ある以上な工程が翌日修理されて正常になっている確率は0.5である.今日ある工程が正常だとして,明日・明後日に異常である確率を求めよ.

この例に出てきたような,「各要素が非負で,各列の合計が1であるような正方行列」をstochastic matrixといいます.stochastic matrixは,ある状態の組があって,その組の中の各状態からその組の中の別の状態へある確率で遷移するとき,その確率をひとつの行列で記述することができます.
また,いま現在その組の中の各状態である確率が,その直前の各状態の確率とstochastic matrixだけで決まるような確率過程を,マルコフ過程(正確には,1次マルコフ過程)といいます.
ある農家の昨年の作付け面積は,田がxアール,畑がyアールであった.
(1)今年は,昨年の田の70%を畑に,畑の30%に振り向ける.今年の田,畑の作付け面積をそれぞれx' アール,畑がy' アールとするとき,x' , y' をx, yで表せ.
(2)来年も,今年の田の70%を畑に,畑の30%を田に振り向ける.来年の田,畑の作付け面積をそれぞれx' 'アール,畑がy' 'アールとするとき,x' ', y' 'をx, yで表せ.

この問題のように,stochastic matrixが「何乗しても同じ」という行列であることがあります.この場合,1回遷移すると,以後ずっとその状態にとどまることを示しています.このようなことは,stochastic matrixが正則でない(逆行列がない)ときに起こります.
また,x, yを平面上の点と考えると,マルコフ過程は平面上の点を一定のルール(stochastic matrixで表される)で移動していく過程と考えられます.このとき,stochastic matrixがこの問題のような行列であると,ある点から出発すると,1回移動した後,以後何度遷移してもその点にとどまることになります.
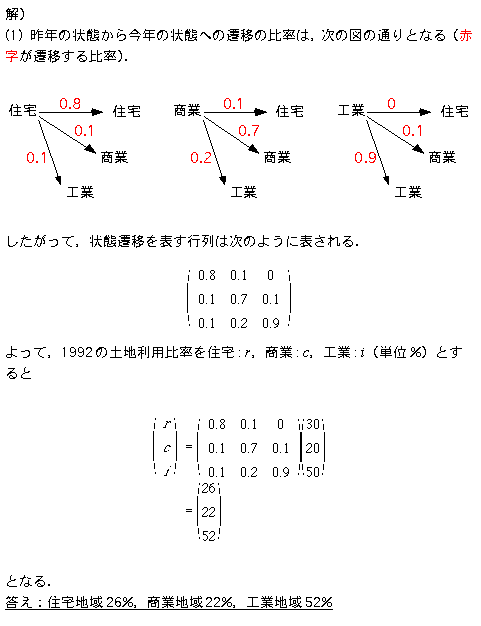
ある都市の1992年の土地利用比率は,住宅地域30%,商業地域20%,工業地域50%であった.また,この5年間に,住宅地域の10%が商業地域に,10%が工業地域に変化し,また商業地域の10%が住宅地域に,20%が工業地域に,さらに工業地域の10%が商業地域に変化した.1997年の土地利用比率を求めよ.
2つのstochastic matrixの積は,やはりstochastic matrixです.したがって,stochastic matrixのべき乗はstochastic matrixです.