行列式は,n行n列の行列から,各行から1つずつ,かつ各列から1つずつになるようにn個の要素をとりだしたもの積の全てを,あるルールで符号を決めて足しあわせたものです.n行n列の行列に対して,このような取り方はn!通りありますから,行列式はn!項の式になります.
各項での符号の決め方は,次のようになります:項の中の各要素に,その要素が属する行の番号をつけます.また,その要素が属する列の番号もつけます.そして,要素を2つ取り出したとき,「行の番号の大小」と「列の番号の大小」とが逆になっている組をさがします.そのような組が偶数個なら項の符号は+,奇数個なら−です.

歴史的には,行列よりも行列式の方が先に研究されています.それは,行列式が連立一次方程式の解に現れるためです.

2元ではなくn元でも同じで,n次の行列式で表示できます.このように行列式で表示すると,次のような定理によって行列式を簡略化して計算できる可能性がでてきます.
以下の定理の証明は,線形代数学の講義の方で習ってください(定理は標語風に書いてあります.正式な表現も習ってください).

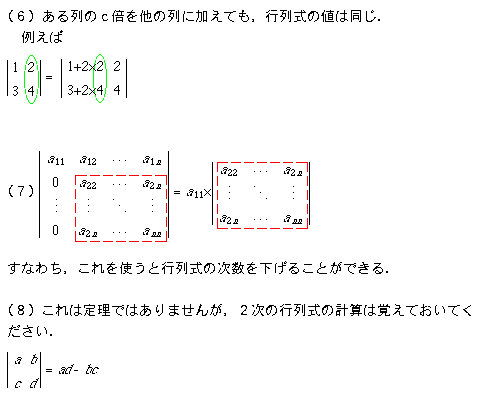
行列式の簡略化は,(x,x,...,x)という同じ値の要素ばかりの行(または列)を作って,これを定理(6)を使って(x,0,...,0)という行(または列)にすると,うまくいくようです.
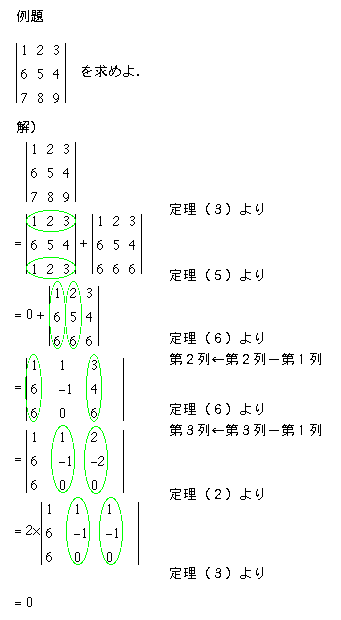

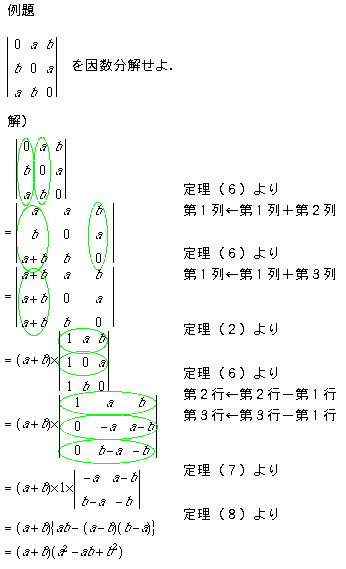
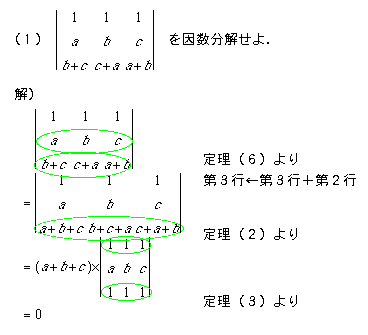
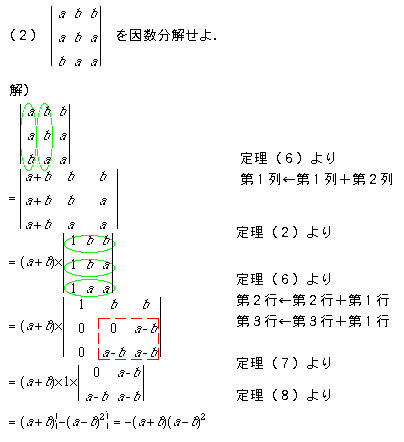
行列式の計算の問題例として,次のような因数分解の問題があります.こういう問題では,(x,x,...,x)という同じ値の要素ばかりの行(または列)を作って,定理2を使ってxを行列式の外に出す,という方針がうまくいくようです.