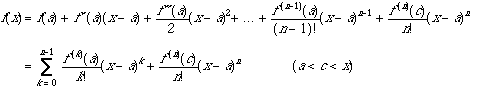基礎数学演習Ｉ　微分学（３）
Taylorの定理

Taylorの定理

　Taylorの定理は，関数f(x)が区間[a, x]でn回微分可能なとき，f(x)をf(a), f'(a), f''(a), ..., f(n)(a)を使ってxの多項式で表す方法を示したものです．f(x)は，下のように表されます．

（＊）

各係数の意味

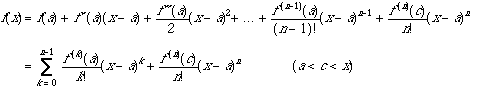　f(x)を(n-1)次の多項式で次のように近似するとします．

このとき，f(a) = a0です．また，

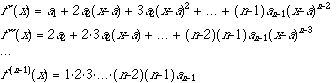
ですから，

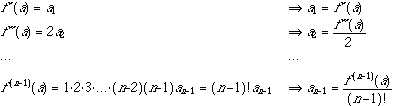
となり，各係数が得られます．

剰余項の意味

　Taylorの定理の展開式（＊）の最後の項は剰余項と呼ばれ，多項式で近似しきれなかった部分が入っています．これがとなることは，平均値の定理を使って証明できます（「微分学」の講義で習ってください）．

ここでは，この剰余項の意味を次のコマ漫画で説明します．

Taylor級数

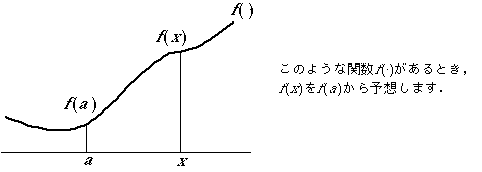
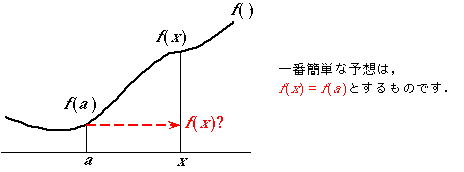
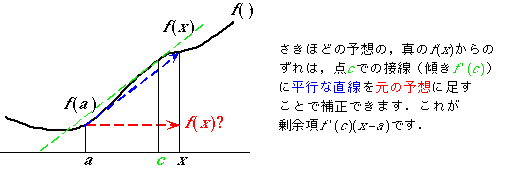
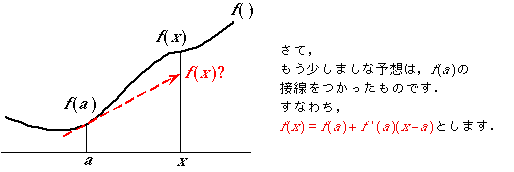
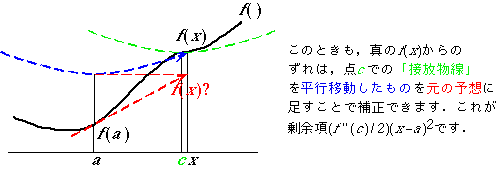
　もし，f(x)が[a, x]で無限回微分可能（C∞級といいます）で，剰余項のn→∞の極限が０，すなわち

ならば，f(x)は下の無限級数で表せます．

これをTaylor級数と呼びます．このことは，「f(a), f'(a), f''(a), ..., f(n)(a), ... が全てわかっていれば，点aでの情報だけをもとにf(x)が復元できる」ことを示しています．

Maclaurinの定理とMaclaurin級数

　Taylor展開の式で，a = 0, c = θxとおくと，cの範囲a<c<xは，θの範囲0<θ<1と同値です．このとき展開式は

となります．これをMaclaurinの定理と呼びます．また，[0,x]で無限回微分可能で，n→∞で剰余項→0なら，

となります．これをMaclaurin展開と呼びます．

例題

（注）ここで， (-∞ < x < ∞) を用いました．この定理はこの手の問題を解くときによく使われます．

問題

提出問題


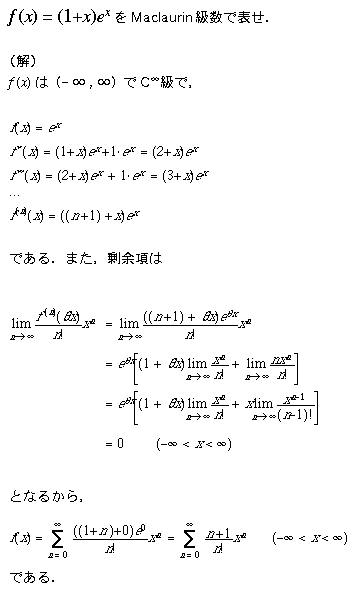
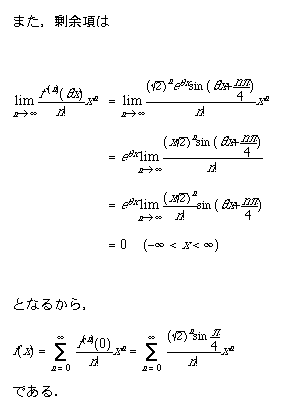
（注）ここで，を用いました．

「基礎数学演習Ｉ」のページへ