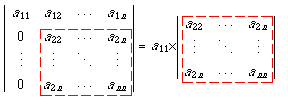
前々回の演習(「行列式」)で,下のような定理(定理(7))を紹介しました.

今回は,この定理を使って行列式を次数が1つ低い行列式の和で表す方法を説明します.
下の例を見てください.
先々週の定理(3)より,3×3の行列式をつぎのように書くことができます.
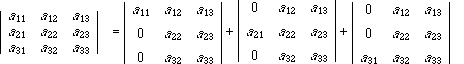
右辺の後ろの2つの行列式を,定理(7)の形にするために,行の入れ換えを行います.このときに,第1行に持って行く行以外の行の順序を変えないことにします.すると,下のような入れ換えを行うことになります.
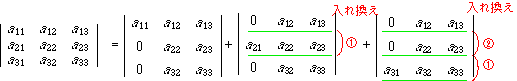
入れ換え後の式は,定理(4)を用いると次のようになります.
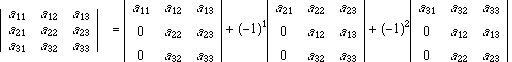
これに定理(7)を用いると,次のように第1列に関する行列式の展開が得られます.
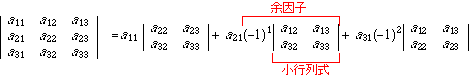
右辺の,元の行列式から行1つ列1つが取り除かれて次数が一つ下がった各行列式を小行列式(左からD11, D21, D31と書く),それに符号をつけたものを余因子(左からA11, A21, A31と書く)といいます.
これを一般的に表すと,行列式|A|の第j列に関する展開は
![]()
となります.各余因子における(-1)の指数は,「その余因子がもとの行列式のi行j列を取り除いてできているとき,指数はi+j」となります.
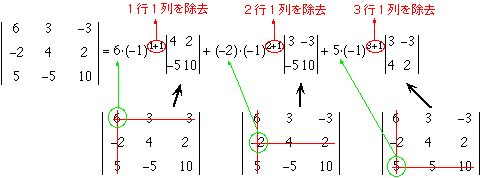

この例のように,行列式の操作によって「0」の要素をつくり,それを含む行(列)で展開すると計算が楽になります.


