基礎数学演習Ｉ　微分学（４）
偏微分と全微分

偏微分

　多変数の関数を，「１つの変数以外をすべて定数と見て，その１つの変数で微分する」ことを，偏微分と呼びます．例えば，２変数の関数f(x,y)があるとき，

f(x,y)をxで偏微分：　

f(x,y)をyで偏微分：　

となります．

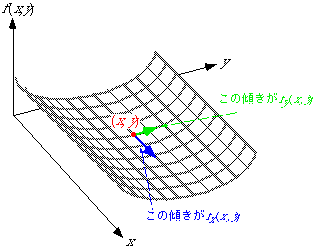f(x,y)が左図のグレーの部分のような形（スノーボード競技のハーフパイプを想像してください）のとき，fx(x,y)とfy(x,y)は(x,y)でのそれぞれ青色，緑色の方向の傾きになります．

例

z = xy をx, yで偏微分すると，

zx = yxy-1　　（yを定数と見る）

zy = xylogx　　（xを定数と見る）

問題

z = logyx をx, yで偏微分せよ．

解）

底をeに変換すると，

であるから，

全微分

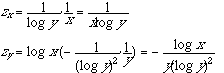
　１変数関数f(・)について，「f(x)がxで微分可能である」とは，Aを定数として

と書けることを言います．同じことを

「がどんな小さなΔxについても成り立つ」

と書くことができます．ただし，q(・)は

となる関数です．つまり，q(Δx)は「Δxが０に近づくとき，Δxよりも速く０に近づく」関数です．このような関数を「o(Δx)」と書くこともあります．

　これと同様に，

「が，どんな小さなΔx, Δyについても成り立つ」

とき，「f(x, y)は全微分可能である」といいます．ただし，q(・)は

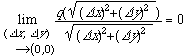
となる関数，つまりです．

「偏微分可能」であることは，x方向あるいはy方向についてのみ微分可能であることしか示していません．しかし，「全微分可能」であることは，Δx, Δyの比率は自由ですから「どの方向にも微分できる」ことを示しています．

　さて，ここでΔy =0とおくと

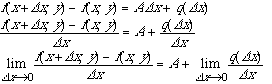
ですから，fx(x,y) = Aとなります．同様に，Δx =0とおくと，fy(x,y) = Bとなります．よって，となります．ここで，(Δx, Δy)→(0, 0)のときとなるので，Δx, Δyが非常に小さいときこれをdx, dyと書くと，

と書くことができます．ここで，f(x+dx, y+dy) - f(x,y)は，xがdxだけ，yがdyだけ微少に変化したときのfの変化量で，これをdf(x, y)と書いて，

をf(x, y)の全微分と言います．

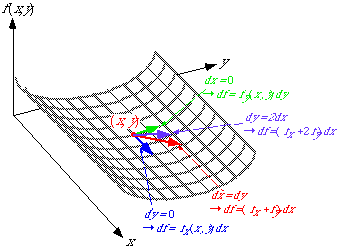ふたたび「ハーフパイプ」を考えてみます．dx=0の場合，dy=0の場合，dx=dyの場合，dy=2dxの場合など，dxとdyがいろいろな比率をとるとき，dfは全微分によってそれぞれ求まります．

例題

　長軸の長さ2a，短軸の長さ2bの楕円の面積をSとする．a, bの測定誤差がそれぞれda, dbの時，Sの誤差はいくらか．

解）

与えられた楕円の面積Sは

である．ここで，Sをa, bで偏微分すると

となる．求めるSの誤差は，Sの全微分dSで，

となる．

提出問題


「基礎数学演習Ｉ」のページへ