前々回の演習で，行列式の展開を説明しました．行列式｜A｜の第j列に関する展開は，i行j列に関する小行列式をDij，余因子をAijとすると，
となります．
では，j≠kのとき，
の値はいくらでしょうか？
ここで，行列式｜A｜の第k列を，第j列と同じ列ベクトルに置き換えた行列式｜A'｜を考えます．｜A'｜を第k列で展開すると，
となりますが，ここで第k列と第j列は同じですから，aik = aij (i = 1, 2, ... , n)で，
となります．ところで，｜A'｜には同じ要素の列が２つあるので，５月１４日の演習で説明した定理の（５）によって，｜A'｜= 0です．
したがって，j≠kのとき，
となります．
以上のことを行列で表示すると，第j行・第j列について
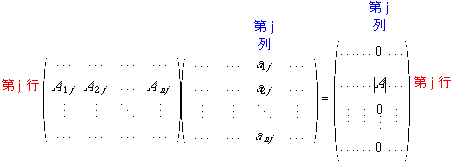
となり，他の行・列も考えると
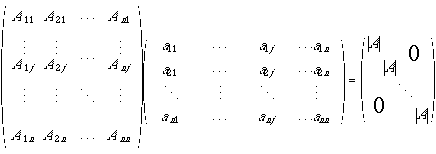
すなわち，Eを単位行列として
とあらわせます．ここで，
で，
を余因子行列といいます．
上の式から，｜A｜≠0のとき，Aの逆行列A-1は，
とあらわされます．
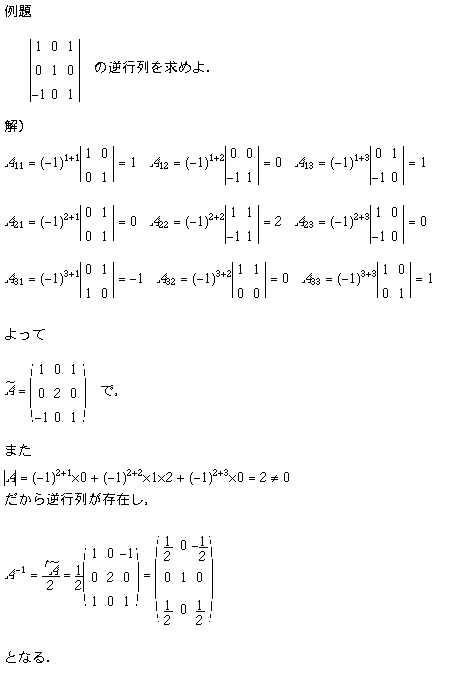
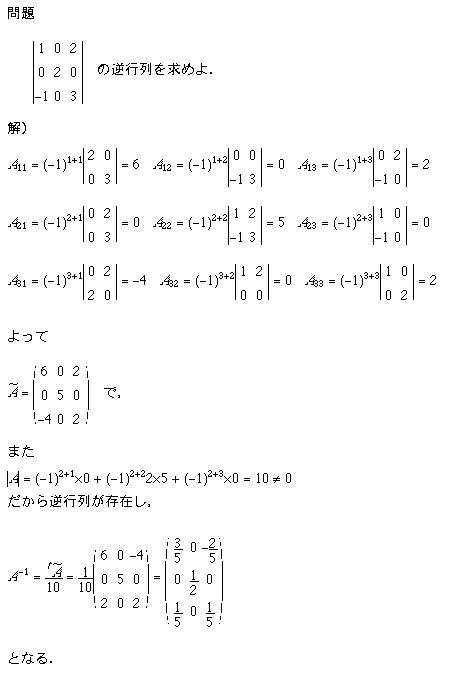
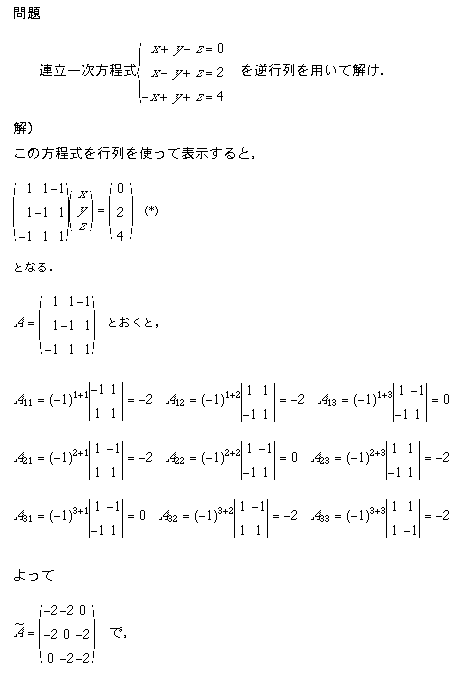
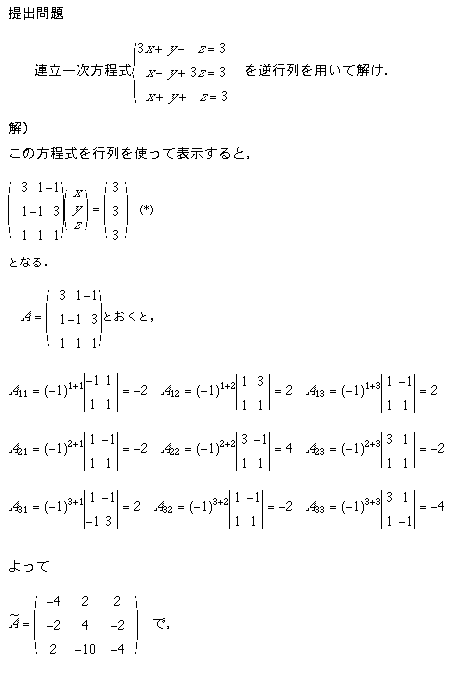
講義中
を余因子行列としましたが，の方が余因子行列です．おわびし，訂正します．