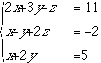
行列の基本変形とは，
の３つの操作をさします．基本変形の意味を，連立方程式を解く作業とならべて考えてみましょう．次の方程式を考えます．
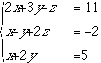
これに対応する行列として，次の行列を考えます．
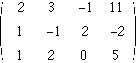
以下，方程式を解く手順と，それに対応する基本変形をならべます（(1)(2)(3)はそれぞれ第１，２，３行を表します．「(1)←(1)＋(2)×２」は「第２行の２倍を第１行に加える」と読んでください．
このように方程式を変形すると，z, y, xの順に解が求まります．このように，基本変形は対応する連立方程式の解を変えない変形のことです．これに対応する行列の方を見ると，下左側に０が集まっています．このような行列を階段行列とよび，段の数を階数（ランク）と呼びます．行列の階数は，基本変形によって変化しません．また，行列Aの階数をrankAで表します．
さて，上の変形で方程式の係数部分を表す行列を見ると，
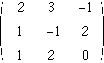から
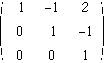のように変形されています．この行列の階数は3で，行列の次数と同じです．このとき，この行列は正則で，この行列によって３次元空間中のある点は別の１点に写像されます．
これに対し，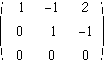
のように階数＜次数の場合は，この行列は正則ではなく，点から点への１対１写像になりません．また，これによって決められる方程式は不定解や不能解になります．
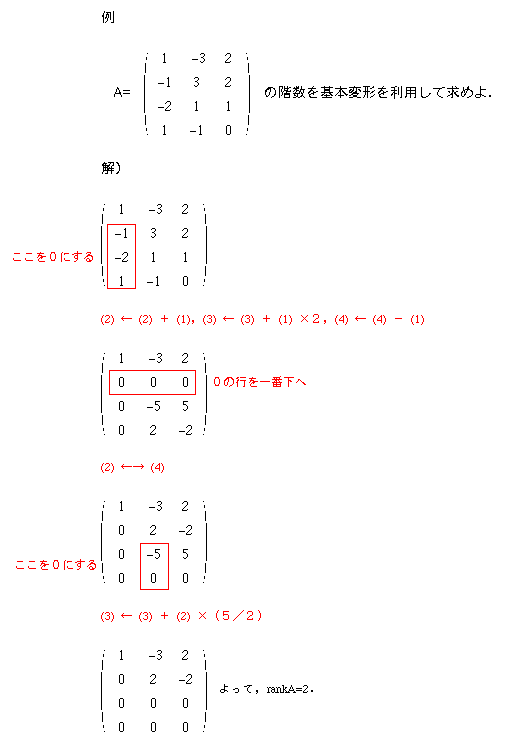
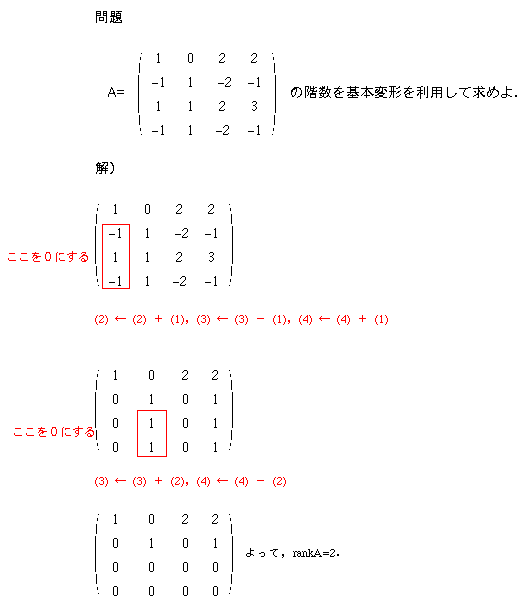
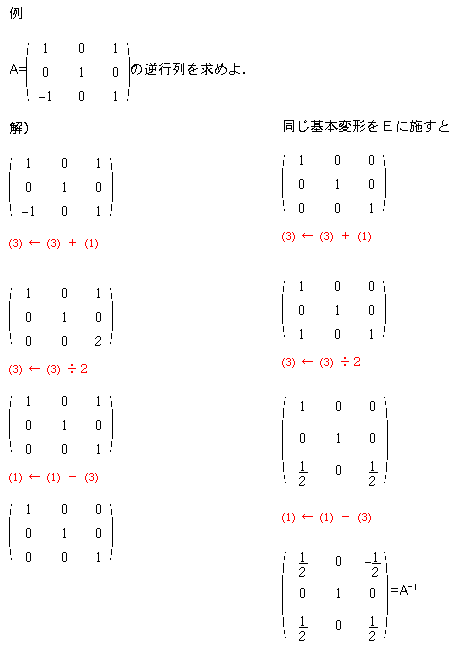
最初の例にあげた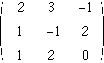から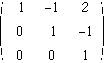への変形の続きを行い，右上部分も０にしてみましょう．
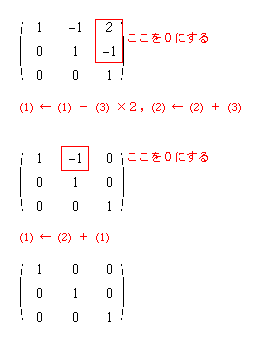
このように，正則な行列は基本変形によって単位行列Eに変形することができます．
ところで，３つの基本変形は，いずれもある正則な行列をかける操作で表現することができます（教科書参照）．そこで，元の行列AからEまでの変形を，それらの行列の積であらわし，それをPとすると，PA=Eと表せます．したがって，P=A-1になります．
A-1=E=PEで，PEとはすなわち「EにPで表される基本変形を施したもの」ですから，「AをEに変形する基本変形と同じ基本変形をEに施すと，A-1に変形される」ことがわかります．
