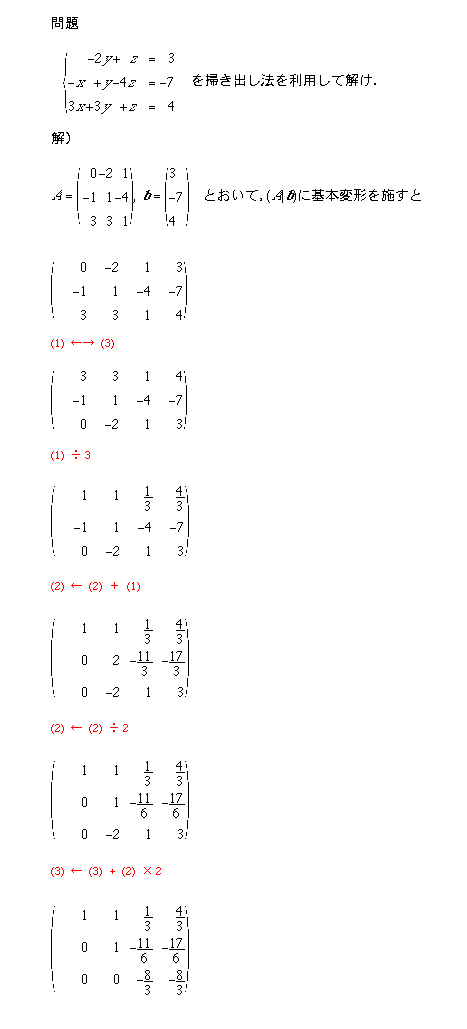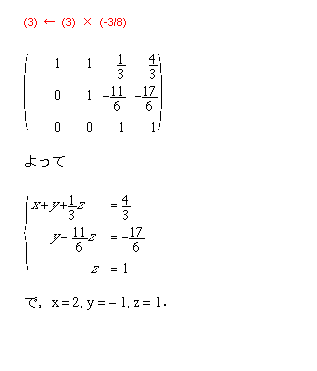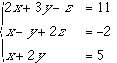
先々週の演習で行ったように,行列の基本変形は連立方程式を解く作業に対応する操作です.先々週と同じ次の方程式をもう一度考えます.
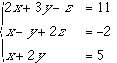
この方程式は,
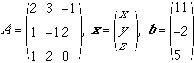
のように行列A,ベクトルx, bを定めると,Ax=bで表されます.このとき,Aとbをくっつけた下のような行列を定義します.
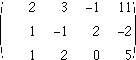
この行列を拡大係数行列といい,(A|b)で表します.先々週の演習で行ったように,拡大係数行列に基本変形を施すことで,連立方程式を解くことができます.この方程式の場合,(A|b)の基本変形を行うと
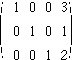
となるので,解はx=3, y=1, z=2となります.このように解が1組に定まるとき,nを未知数の数とすると,rankA = rank(A|b) = nになっています.
別の例として
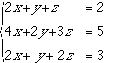
の場合はどうでしょうか.この場合,(A|b)は
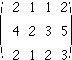
で,これに基本変形を施すと
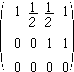
となります.これは
![]()
を意味しており,その解は,cを任意定数とするとき,x=(1-c)/2,y=c,z=1という「不定解」になります.このとき,rankA = rank(A|b) < nになっています.
また,
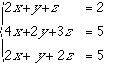
の場合は,(A|b)は
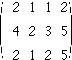
で,これに基本変形を施すと
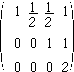
となります.これは
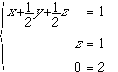
を意味しており,3行目を見てわかるように,この方程式は「不能」です.このとき,rankA < rank(A|b) になっています.
このような,行列の基本変形を用いた連立一次方程式の解法を「掃き出し法」と呼びます.